
“Effective Velocity” is a term that has been around for more than a decade. Its theory has become popularized by Perry Husband.
It’s an idea on pitch sequencing; that a pitch is “effectively” at a higher/lower velocity depending on the location. The idea has been approved throughout the baseball community, particularly the so-called “old-school” coaches and commentators.
In 2019, Dan Aucoin(Manager of Driveline R&D Operations) released an article, investigating and “debunking” this theory with MLB’s public data set, and their internal HitTrax batted-ball data collected from professional hitters.
In this post, I attempt to further investigate the Effective Velocity and (in)validating its legitimacy, using possibly new theories and calculations.
Table of Contents
1. The Original Theory
Claims
2. Counterstatements
Driveline’s Article
Kyle Boddy’s View
3. 3 Key Missing Details
Tunneling
“Actual” Reference Contact Point
A Missing Variable
4. “True” Effective Velocity – Rotational
Variables
Calculations
5. “True” Effective Velocity – Linear
Variables
Calculations
6. Validating Claims and Incorporating Effective Velocity
Offensive Production Peaks at 90 EV-mph
Meaning of ±6 EV mph
Fallacies in Analyzing Effectiveness
Hard Up&In, Soft Down&Away
7. Conclusion
The Effective Velocity Theory

Because the barrel has to be more out-front for a pitch up&in, the hitter has to swing earlier. The opposite is true for a pitch down&away. The effective velocity difference between those two pitches is 8-10 mph. In other words, a 90 mph down&away is more like 85 mph, and a pitch up&in is more like 95 mph.
The idea is to use that difference to sequence pitches better. By throwing pitches to different speeds and locations, and creating time disruptions in different ways.
Claims
The main EV-claims (mainly by Perry Husband) include the following:
- Offensive production peaks at 90 EV mph
- Production significantly increases when the consecutive pitch is within +/- 6 EV mph
- The best pitchers abide by EV principles
Counterstatements
Driveline’s Article
In 2019, Dan Aucoin wrote an article, INVESTIGATING EFFECTIVE VELOCITY AT THE MLB LEVEL, in an attempt to (in)validate the Effective Velocity theory with Driveline’s Research & Development team. It is unclear who the exact personnel were, or if it was Dan Aucoin’s independent research.
Here’s a snippet:
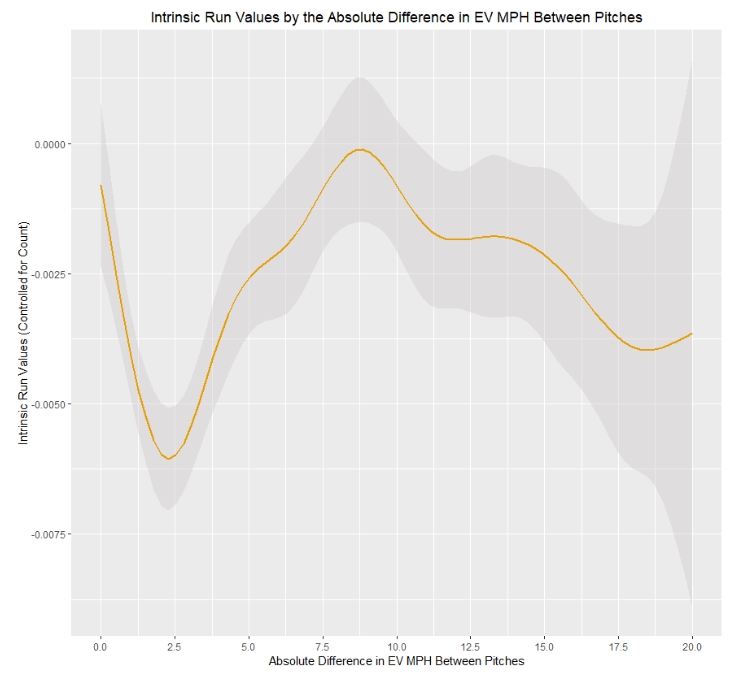
The team calculated Intrinsic Run Values based on the EV mph difference between 2 consecutive pitches.
The findings were that: A. Exit Velocity, xwOBAcon, and HR Rate slightly increased on pitches thrown within 6 EV MPH of the previous pitch, and B. Once count and other context was accounted for, batter production increased against pitches thrown outside the 6 EV MPH threshold.
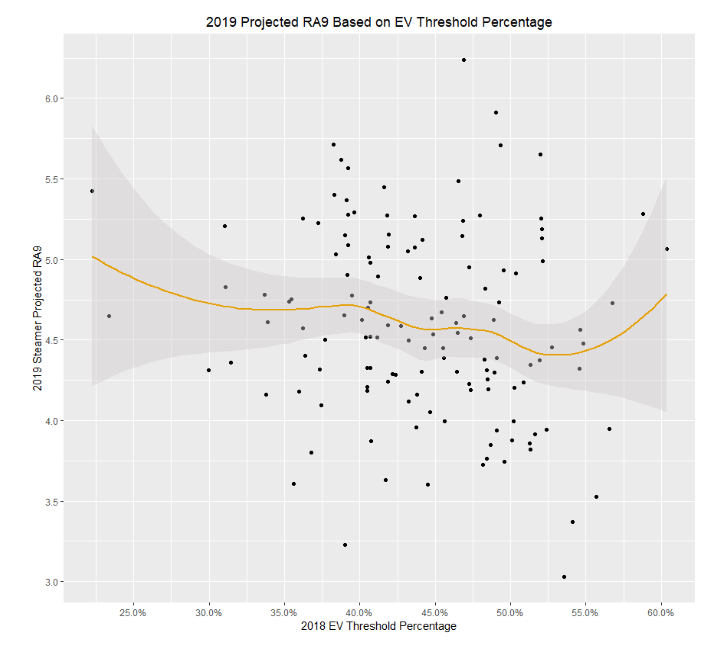
They also ran a correlational study to find if pitchers who abide by EV principles perform better than pitchers who don’t.
The finding was that there are weak correlations between performance and EV metrics for pitchers with at least 100 pitches thrown.
The team then went on to validate if the pitches are actually (effectively)faster/slower in the particular location; if contact was made further ahead for pitches up&in, in and behind for pitches down&away.
The contact points turned out to be true. However, when the reaction time was calculated to adjust for the estimated point of contact, the actual mph adjustments weren’t as impressive as expected:
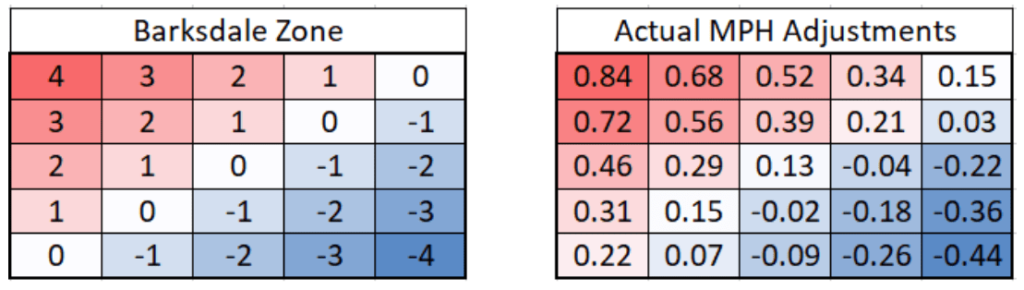
The total EV mph difference in-zone was calculated to be closer to 1.25mph rather than 8-10mph.
The team also did further correlational studies to find that “Effective Velocity did not describe performance more accurately than release speed.” Dan Aucoin claimed that “pitchers predominately throw to areas of the strike zone that complement their movement profile, rather than to add velocity to their fastball.”
*Make sure to read the full post to limit misrepresentations.
Kyle Boddy’s View
Now, because it is unclear who was behind the research above, it was unclear whether this article was approved, nor if it was backed by other researchers(which does not make the material more true, but more appealing). I searched through google to see if there’s prominent personnel in the data-driven baseball community endorsing this idea.
I found (Founder of Driveline Baseball)Kyle Boddy’s Reddit AMA that was held in May of 2021. For one of the questions that asked him what he thinks of the EV theory, he answered:
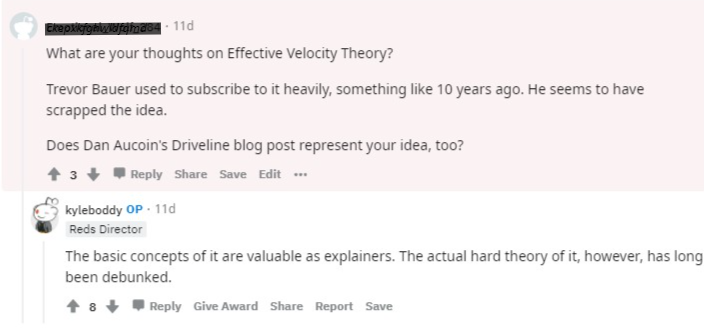
Given his influence over the data-driven baseball community, it seems logical to assume that this theory is no longer universally accepted.
3 Key Missing Details
While acknowledging the depth of investigation(40min reading time!) of this article, I would like to point out three key missing details that may dispute the article and revalidate the theory of Effective Velocity.
Tunneling
A key mistake in running correlational studies for the effectiveness of EV-diff. is to leave out tunneling, which is indeed what happened in Driveline’s research.
I am confident there is no debate on the importance of tunneling. To neglect tunneling in measuring an individual pitch’s effectiveness in discussing EV effectiveness would be no different than saying “Curveball yanked to the other batter’s box is the most effective because it has the most location-difference for the hitter to adjust”.
(Perry Husband “came up” with the concept of EV Tunneling, although it seems no different than just tunnelling, frankly.)
While, I understand it is quite difficult to measure tunneling for each individual pitch sequencing for every at-bat when dealing with thousands. I also understand that the study was designed upon the claim of “more EV-diff. = good”, to (in)validate it specifically.
“Actual” Reference Contact Point
Another (perhaps insignificant) error may be an inaccurate measurement of reference point-of-contact.
The Driveline team used average contact point, which I would argue is a sub-optimal reference.
Average BIP contact does not consider the quality of contact; the only qualification is to “be in play”. For a bunt, the depth of contact would be (almost)identical, regardless of timing, quite frankly. This may be a bad example, but the point comes across: in the case where the hitter was “late” up&in(thus not making contact out front enough), the contact point data would consider it like any other BIP.
It would be reasonable to assume that on average, hitters are late for faster pitches(up&in) and early for slower pitches(down&away). That is likely the reason why “actual mph adjustment” is nearly double for the pitch up&in(0.84) than the pitch down&away(0.44): When the bat is late up&in, it will still likely make contact. When the bat is early down&away, it will “run out of barrel” and miss.
I would rather argue that the reference point should be the point of optimal(middle) contact, which would likely be the point of highest average exit velocity. This is with the premise that the hitter makes optimal contact middle-middle.
If the above is true, how much of a difference would be made? I would guess, 2-2.5 mph instead of 1.25 mph.
A Missing Variable in the Equation
The theory of Effective Velocity is essentially an idea that the optimal contact point is different depending on the pitch’s 2D location.
Then we’ve found out that for a pitch up&in, the optimal contact point is more out-front, with the opposite being true for a pitch down&away, due to the fact that hitting is a rotational movement.
Then we’ve found out that it takes a shorter amount of time for the ball to get to the up&in optimal contact point, with the opposite being true for a pitch down&away.
What we’ve forgotten, is that it takes a longer time for the bat to get to the up&in optimal contact point, with the opposite being true for a pitch down&away. Because hitting is rotational. Unlike bunting. Even if the ball arrives at the up&in / down&away optimal contact point at the same time, the hitter will more likely be late for the former, and early for the latter.
Below is the calculation for this difference:
“True” Effective Velocity – Rotational
This calculation measures the amount of additional time the barrel takes to arrive at the up&in optimal contact point from down&away optimal contact point.
They’re simple physics you learn in high school. In other words, it’s the best I could possibly do with physics.
Variables
Given: At t=0s, the barrel is ‘at’ the down&away optimal contact point
Given: The distance between the ‘center of rotation’ and the ‘barrel’ is 1m(*39.4in), r=1m
Given: The barrel’s ‘linear’ velocity is 31.3m/s(*70mph)^ ^, v=31.3m/s
Given: The rotation happens across 60°(2/3 baseball diamond, since hitters “pull”), Δθ=1.05rad
Assume: Swing is completely rotational
Assume: The barrel doesn’t slow down, a=0
*Obviously, this is an extremely simplistic estimation. No swing is completely rotational, and body parts move in a sequence. The numbers are most likely inaccurate(but acceptable), and they’re subject to change for every hitter.
Calculations
w(Angular Velocity) = v/r
w = 31.3 ÷ 1
Δθ ÷ Δt = 31.3, Δθ ÷ 31.3 = Δt
(1.05) ÷ 31.3 = 0.0335s = Δt
Using Alan Nathan’s Trajectory Calculator, I found that for a 90 mph pitch, the pitch up&in would be 7-8 mph “effectively” faster considering the swing only, and combined with the ball trajectory difference, the total difference would be around 10 mph.
*I originally expected the number to be 6 mph or below, and these results surprise me, personally. Even with the outcome, it’s still hard for me to accept it.
“True” Effective Velocity – Linear
Because that last calculation gave a somewhat unbelievable output, I decided to make a different one for the sake of it.
This calculation essentially assumes that the batter’s swing up&in is no different, rotationally, than the swing down&away. In other words, we are assuming that the only difference in time comes from the depth of contact.
Variables
Given: At t=0s, the barrel is ‘at’ the down&away optimal contact point
Given: Up&in point of contact is 0.5m(*20in) ahead of down&away point of contact, Δd=0.5m
Given: The barrel’s ‘linear’ velocity is 31.3m/s(*70mph), v=31.3m/s
Assume: Swing is completely linear
Assume: The barrel doesn’t slow down, a=0
Calculations
Δt = Δd ÷ v
Δt = 0.5 ÷ 31.3 = 0.0160s
(Again using Alan Nathan’s Trajectory Calculator) For a 90 mph pitch, the pitch up&in would be 3-4 mph “effectively” faster considering the swing only. Combined with the ball trajectory difference, the total difference would be around 6 mph.
The output of this equation feels more correct, to me(should never be trusted). Although, assuming that the barrel moves completely straight, is quite deviated from reality, so the equation’s validity is close to 0.
**If you are uncomfortable with the givens or calculations, please tell me. I am trying my best to fix & improve any flaws.
Validating Claims and Incorporating Effective Velocity
After all, does it matter?
Perhaps.
It’s been less than a decade since the notion that “movement is just as important as velocity” became widely accepted in the baseball community. Ethan Moore’s QOP model actually values vertical movement of the Fastball more than velocity.
Perhaps this method of adding/subtracting velocity might not be as effective as actual velocity. Hitters could be adjusting differently based on the location. Perhaps 85mph down&away is the same as 90 mph middle-middle, because hitters expect it.
Despite having scientific evidence for the existence of EV, we still have yet to find clear-evidences of the effectiveness of EV-pitching.
Fourseam Fastball up&in may be “faster” than up&away, but it clearly misses fewer bats as the ball naturally falls on the bat path.
Let’s revisit the EV theory’s claims:
Offensive Production Peaks at 90 EV-mph
The logic/evidence behind this claim is weak-to-none. The number seems arbitrary, and it doesn’t have a strong relationship with the EV theory, either.
Meaning of ±6 EV mph
If this refers to an end-EV difference, it would hold little water, as most secondary pitches are already 6+ mph apart from the Fastballs.
If it rather refers to the EF-effect difference, in other words, generated difference, it would essentially implicate location differences. Then, the claim would really be “up&in, down&away combo is effective regardless of the velocities.” That would be nonsense.
Fallacy in Analyzing Effectiveness
Perhaps we’ve been confused away from the correct way to validate EV-effects.
The most serious complication with the overall EV theory is Perry Husband’s over-application, which takes away a lot of clarity. (This statement has no intention against his personal being.)
EV theory isolates timing as the only factor and tries to apply that to every scenario, and attributes any pitcher’s success to using EV principles. In reality, there are multiple effects to be used to generate outs, not one.
Trying to explain how a Sinker is effective using effective velocity wouldn’t work. It would also be impossible to explain how a Slider up-in-the-zone is effective. Trying to mould them into EV-narrative would be non-sensical, nor would it be mostly valid.
There are countless successful pitchers who had their success without influencing the hitters’ timing. Most prominent examples include Clayton Kershaw, Zack Greinke, Corey Kluber, and countless closers with 1-2 pitches.
Hard Up&In, Soft Down&Away
After, if there could be an utmost significant piece of evidence that can only be explained by effective velocity, it would be the fact that the majority of hitters have a weakness against hard up&in, soft down&away combo.
This combo is quite a traditional one. (Although conventional wisdom may not be the most factual, the fact that this pattern has seemed to work, for a long time, tells something.) And it is very difficult to prove how that combo is effective without the EV theory–I have failed to come up with one myself.
Within the strike zone, pitch movement parallel to the bat is normally inferior compared to perpendicular, as the break goes in-line with the bat path to never actually miss it. Unless that movement leads to a difference in effective velocity, it isn’t clear how it’s necessarily effective, if effective at all.
Now, there can be a case to be made that the barrel isn’t long enough to cover the whole diagonal line. Then, however, we have to figure out why slower is better down&away because the movement effect would be worse slower.
Conclusion
The results in this study finds that Effective Velocity is real, and the difference may be significant.
However, clear evidence of Effective Velocity being as effective as Actual Velocity is yet to be found, and how to best optimize pitch sequencing with EV is unknown.
If you found this post interesting, you can read more of my baseball posts here.

I’m curious who the author is……….. ?? A recent 3rd party independent University study of Effective Velocity has proven that timing stats actually do peak at one EvMPH…..AND…….. the study proved that there was a 6 EvMPH range of speed the timing based stats were highest, with a fairly sharp drop just beyond 3 EvMPH on either side of the peak. In 2004, the peak for timing stats was 90 EvMPH and now it is about 92.5 EvMPH, due to the increases in pitch velocity that makes perfect sense. You pointed out several very good points that Driveline ignored but you left out multiple layers of Effective Velocity. This indicates you have about a ‘Blue Belt’ level of understanding of Effective Velocity. Still, props for the updated viewpoint and the nuances you did catch.